PyTorch Neural Networks#

PyTorch is a Python package for defining and training neural networks. Neural networks and deep learning have been a hot topic for several years, and are the tools underlying many state-of-the art machine learning tasks. There are many industrial applications (e.g. at your favorite or least favorite companies in Silicon Valley), but also many scientific applications including

  • Processing data in particle detectors

  • Seismic imaging / medical imaging

  • Accelerating simulations of physical phenomena

  • …

A (deep) feed-forward neural network is the composition of functions \begin{equation} f_N(x; w_N, b_N) \circ f_{N-1}(x; w_{N-1}, b_{N-1}) \circ \dots f_0(x; w_0, b_0) \end{equation} where each \(f_i(x; w_i, b_i)\) is a (non-linear) function with learnable parameters \(w_i, b_i\). There are many choices for what the exact function is. A common and simple one to describe is an (affine) linear transformation followed by a non-linearity. \begin{equation} f_i(x; w_i, b_i) = (w_i \cdot x + b_i)_+ \end{equation}

where \(w_i \cdot x\) is matrix-vector multiplication, and \((\cdot)_+\) is the ReLU operation (Rectified Linear Unit) \begin{equation} x_+ = \begin{cases} x & x > 0\ 0 & x \le 0 \end{cases} \end{equation}

If you take the composition of several functions like this, you have a multilayer perceptron (MLP).

Deep Learning Libraries#

There are many deep learning libraries available, the most common ones for python are

  • TensorFlow, Keras

  • PyTorch

Working with tensorflow requires going into lot of details of the contruction of the computation graph, whereas Keras is a higher level interface for tensorflow. Tensorflow is very popular in the industry and good for production code.

PyTorch can be used as low level interface, but is much more user-friendly than tensorflow, but it also has a higher level interface. Pytorch is more popular in the research community.

Main features that any deep learning library should provide#

No matter what library or language you use, the main features provided by a deep learning library are

  1. Use the GPU to speed up computation

  2. Ability to do automatic differentiation

  3. Useful library functions for common architectures and optimization algorithms

PyTorch#

We will look at all of the above in pytorch. The best way to think about pytorch is that its numpy + GPU + autograd.

You can install it with

conda install pytorch.

Alternatively (and recommended), run this notebook in Google Colab– it provides an environment with all of the PyTorch dependencies plus a GPU free of charge.

import torch
import numpy as np
import matplotlib.pyplot as plt
torch.__version__

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 import torch
      2 import numpy as np
      3 import matplotlib.pyplot as plt

ModuleNotFoundError: No module named 'torch'

Automatic Differentiation#

Automatic differentiation is different from numerical differentiation, which requires a choice of step size, and symbolic differentiation which creates a single expression for a derivative. Instead it performs chain rule repeatedly.

PyTorch uses dynamic computation graphs to compute the gradients of the parameters.

x = torch.tensor([2.0])
m = torch.tensor([5.0], requires_grad = True)
c = torch.tensor([2.0], requires_grad = True)

y = m*x + c
y

tensor([12.], grad_fn=<AddBackward0>)

Define an error for your function

loss = torch.norm( y - 13)
loss

tensor(1., grad_fn=<CopyBackwards>)

m.grad

Calling x.backward() on any tensor forces pytorch to compute all the gradients of the tensors used to compute x which had the requires_grad flag set to True. The computed gradient will be stored in the .grad property of the tensors

loss.backward()

m.grad

tensor([-2.])

c.grad

tensor([-1.])

with torch.no_grad():
    m -= 0.01 * m.grad
    c -= 0.3 * c.grad

m,c

(tensor([5.0200], requires_grad=True), tensor([2.3000], requires_grad=True))

m.grad, c.grad

(tensor([-2.]), tensor([-1.]))

m.grad.zero_()
c.grad.zero_()

m.grad, c.grad

(tensor([0.]), tensor([0.]))

y = m*x + c
y

tensor([12.3400], grad_fn=<AddBackward0>)

loss = torch.norm( y - 13)
loss

tensor(0.6600, grad_fn=<CopyBackwards>)

loss.backward()
m.grad, c.grad

(tensor([-2.]), tensor([-1.]))

Making it more compact#

def model_fn(x,m,c):
    return m*x + c

def loss_fn(y,yt):
    return torch.norm(y-yt)

m = torch.tensor([5.0], requires_grad = True)
c = torch.tensor([2.0], requires_grad = True)

x = torch.tensor([2.0])
yt = torch.tensor([13.0])

y = model_fn(x,m,c)
loss = loss_fn(y,yt)
loss.backward()
with torch.no_grad():
    m -= 0.05 * m.grad
    c -= 0.05 * c.grad
m.grad.zero_()
c.grad.zero_()

print( f" m = {m}\n c = {c}\n y = {y}\n loss = {loss}")
#note that 'loss' indicates the loss for the previous m,c values

 m = tensor([5.1000], requires_grad=True)
 c = tensor([2.0500], requires_grad=True)
 y = tensor([12.], grad_fn=<AddBackward0>)
 loss = 1.0

Here’s an explicit loop:

x = torch.randn(5,100)
yt = torch.randn(1,100)
losses = []

for i in range(100):
    y = model_fn(x,m,c)
    loss = loss_fn(y,yt)
    loss.backward()
    with torch.no_grad():
        m -= 0.05 * m.grad
        c -= 0.05 * c.grad
    m.grad.zero_()
    c.grad.zero_()

    losses+=[loss.item()]
    print( f"loss = {loss}")

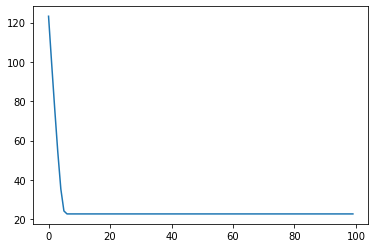
plt.plot(losses);

loss = 123.2157211303711
loss = 99.48639678955078
loss = 76.33134460449219
loss = 54.369239807128906
loss = 35.38062286376953
loss = 24.25409507751465
loss = 22.751705169677734
loss = 22.747961044311523
loss = 22.747936248779297
loss = 22.747936248779297
loss = 22.747936248779297
loss = 22.747936248779297
loss = 22.74793243408203
loss = 22.747934341430664
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
loss = 22.74793243408203
../_images/17dfd0f7cd33710f9214ee9aa5b3fface8261addd67775be71fc1b3f76134abf.png

Using Library functions#

The subpackage torch.nn provides an object-oriented library of functions that can be composed together.

model = torch.nn.Sequential(
    torch.nn.Linear(5, 5), # 5 x 5 matrix
    torch.nn.ReLU(),       # ReLU nonlinearity
    torch.nn.Linear(5, 5), # 5 x 5 matrix
)

list(model.parameters())

[Parameter containing:
 tensor([[ 0.3316,  0.1522,  0.2492, -0.2992,  0.4102],
         [-0.3598,  0.1222, -0.3902, -0.2934, -0.3457],
         [-0.2198,  0.2152,  0.3994, -0.3181, -0.0516],
         [-0.2023,  0.0867,  0.3717,  0.1664, -0.2102],
         [ 0.4042, -0.3993, -0.3191, -0.2141, -0.2772]], requires_grad=True),
 Parameter containing:
 tensor([-0.4013,  0.2950,  0.1151, -0.2628,  0.2941], requires_grad=True),
 Parameter containing:
 tensor([[-0.3463,  0.3572,  0.3492, -0.3008, -0.2829],
         [ 0.2310, -0.4222,  0.3614, -0.2791, -0.0441],
         [ 0.3478,  0.1490, -0.2911,  0.3047, -0.2649],
         [-0.1012,  0.0829, -0.4061,  0.2447,  0.3126],
         [ 0.2993,  0.0131,  0.1135, -0.3588,  0.2828]], requires_grad=True),
 Parameter containing:
 tensor([-0.2317, -0.3994,  0.1748,  0.2988, -0.1613], requires_grad=True)]

loss_fn = torch.nn.MSELoss(reduction='sum')

In this case, we’ll just fit the model to random data.

x = torch.randn(100,5)
yt = torch.randn(100,5)
losses = []

Optimizers in torch.optim implement a variety of optimization strategies. Almost all are based on gradient descent, since forming Hessians is prohibitive.

optimizer = torch.optim.Adam(model.parameters(), lr=0.03)

for i in range(100):
    y = model(x)
    loss = loss_fn(y,yt)
    loss.backward()

    optimizer.step()
    optimizer.zero_grad()

    losses+=[loss.item()]
    print( f"loss = {loss}")
    
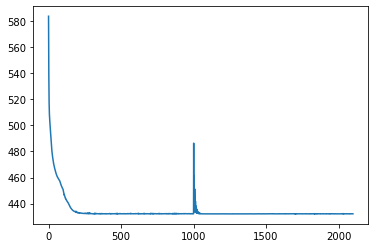
plt.plot(losses);

loss = 432.11285400390625
loss = 432.1269226074219
loss = 432.1133728027344
loss = 432.1142578125
loss = 432.1257019042969
loss = 432.1229248046875
loss = 432.13800048828125
loss = 432.10772705078125
loss = 432.1046447753906
loss = 432.154541015625
loss = 432.12225341796875
loss = 432.10784912109375
loss = 432.1551513671875
loss = 432.1158142089844
loss = 432.1353454589844
loss = 432.1211242675781
loss = 432.1257019042969
loss = 432.11083984375
loss = 432.12322998046875
loss = 432.0851745605469
loss = 432.0941162109375
loss = 432.1318054199219
loss = 432.1329345703125
loss = 432.130859375
loss = 432.1982116699219
loss = 432.1083679199219
loss = 432.2474060058594
loss = 432.24249267578125
loss = 432.15167236328125
loss = 432.2353515625
loss = 432.1801452636719
loss = 432.15069580078125
loss = 432.195068359375
loss = 432.19140625
loss = 432.1322021484375
loss = 432.28363037109375
loss = 432.14068603515625
loss = 432.22784423828125
loss = 432.1725769042969
loss = 432.1201171875
loss = 432.16229248046875
loss = 432.13134765625
loss = 432.1106872558594
loss = 432.1211242675781
loss = 432.1227111816406
loss = 432.13153076171875
loss = 432.1420593261719
loss = 432.125732421875
loss = 432.1514587402344
loss = 432.11346435546875
loss = 432.14105224609375
loss = 432.1415710449219
loss = 432.11651611328125
loss = 432.12127685546875
loss = 432.1683349609375
loss = 432.10308837890625
loss = 432.13079833984375
loss = 432.0877990722656
loss = 432.15673828125
loss = 432.17340087890625
loss = 432.1541748046875
loss = 432.11273193359375
loss = 432.15594482421875
loss = 432.1427917480469
loss = 432.1169128417969
loss = 432.10809326171875
loss = 432.1319885253906
loss = 432.1121520996094
loss = 432.1141357421875
loss = 432.1002197265625
loss = 432.09686279296875
loss = 432.155029296875
loss = 432.1081848144531
loss = 432.1214599609375
loss = 432.11688232421875
loss = 432.1337585449219
loss = 432.13427734375
loss = 432.1278076171875
loss = 432.18560791015625
loss = 432.2113952636719
loss = 432.0914611816406
loss = 432.1741027832031
loss = 432.17205810546875
loss = 432.1813049316406
loss = 432.166748046875
loss = 432.22247314453125
loss = 432.14013671875
loss = 432.1714172363281
loss = 432.14459228515625
loss = 432.1617431640625
loss = 432.11053466796875
loss = 432.1317443847656
loss = 432.16522216796875
loss = 432.1226501464844
loss = 432.1714782714844
loss = 432.15087890625
loss = 432.13763427734375
loss = 432.167236328125
loss = 432.12109375
loss = 432.1177062988281
../_images/6835fad184b0f65f83f02687694752c0a9567a99faa617adee972ccdfe705470.png

MNIST Example#

First, you’ll want to install the torchvision package - this is a package for PyTorch that provides a variety of computer vision functionality.

The MNIST data set consists of a collection of handwritten digits (0-9). Our goal is to train a neural net which will classify the image of each digit as the correct digit

conda install torchvision -c pytorch

import torchvision

from torchvision.datasets import MNIST

data = MNIST(".",download=True)

len(data)

60000

import numpy as np
img,y = data[np.random.randint(1,60000)]
print(y)
img

1
../_images/96d0b7c1ea0443f72ce564923517bcdbc403a6d88cba95735e7991cfa0b991e8.png 
data.train_data[2].shape

/home/brad/miniconda3/envs/pycourse/lib/python3.8/site-packages/torchvision/datasets/mnist.py:58: UserWarning: train_data has been renamed data
  warnings.warn("train_data has been renamed data")

torch.Size([28, 28])

data.train_labels[2]

/home/brad/miniconda3/envs/pycourse/lib/python3.8/site-packages/torchvision/datasets/mnist.py:48: UserWarning: train_labels has been renamed targets
  warnings.warn("train_labels has been renamed targets")

tensor(4)

MNIST Training#

model = torch.nn.Sequential(
    torch.nn.Linear(784, 100),
    torch.nn.ReLU(),
    torch.nn.Linear(100, 100),
    torch.nn.ReLU(),
    torch.nn.Linear(100, 10),
)

loss_fn = torch.nn.CrossEntropyLoss()

sample = np.random.choice(range(len(data.train_data)),1000)
x = data.train_data[sample].reshape(1000,-1).float()/255
yt = data.train_labels[sample]

x.shape,yt.shape

(torch.Size([1000, 784]), torch.Size([1000]))

optimizer = torch.optim.Adam(model.parameters(), lr=0.03)
losses = []

for i in range(100):
    
    sample = np.random.choice(range(len(data.train_data)),1000)
    x = data.train_data[sample].reshape(1000,-1).float()/255
    yt = data.train_labels[sample]
    
    y = model(x)
    loss = loss_fn(y,yt)
    loss.backward()

    optimizer.step()
    optimizer.zero_grad()

    losses+=[loss.item()]
    #print( f"loss = {loss}")
plt.plot(losses);
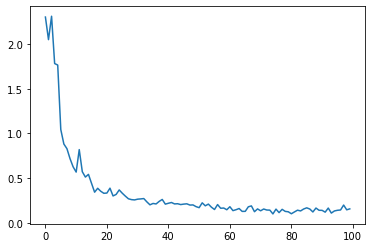
../_images/6244caa3d4d3823cc653db6592d4acc5e3b8d15d82c7c6faaaab9c5b8f10ce61.png 
x_test = data.train_data[-1000:].reshape(1000,-1).float()/255
y_test = data.train_labels[-1000:]

with torch.no_grad():
    y_pred = model(x_test)

print("Accuracy = ", (y_pred.argmax(dim=1) == y_test).sum().float().item()/1000.0)

Accuracy =  0.978

Credits#

This notebook was adapted from a notebook from CME 193 at Stanford