Nearest Neighbors

Given a point cloud, or data set \(X\), and a distance \(d\), a common computation is to find the nearest neighbors of a target point \(x\), meaning points \(x_i \in X\) which are closest to \(x\) as measured by the distance \(d\).

Nearest neighbor queries typically come in two flavors:

1. Find the k nearest neighbors to a point x in a data set X

2. Find all points within distance r from a point x in a data set X

There is an easy solution to both these problems, which is to do a brute-force computation

Brute Force Solution

import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
import scipy.spatial
import scipy.spatial.distance as distance

n = 1000
d = 2
X = np.random.rand(n,d)
plt.scatter(X[:,0], X[:,1])
plt.show()

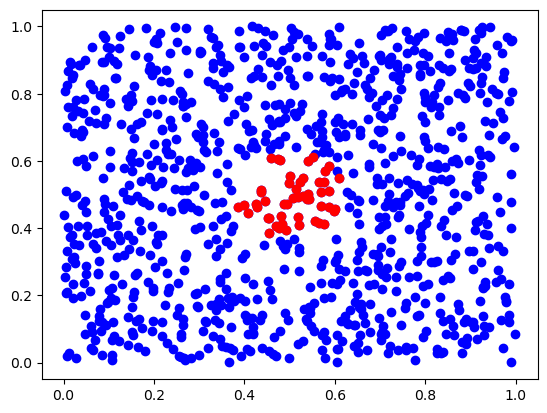
def knn(x, X, k, **kwargs):
    """
    find indices of k-nearest neighbors of x in X
    """
    d = distance.cdist(x.reshape(1,-1), X, **kwargs).flatten()
    return np.argpartition(d, k)[:k]

x = np.array([[0.5,0.5]])

inds = knn(x, X, 50)
plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

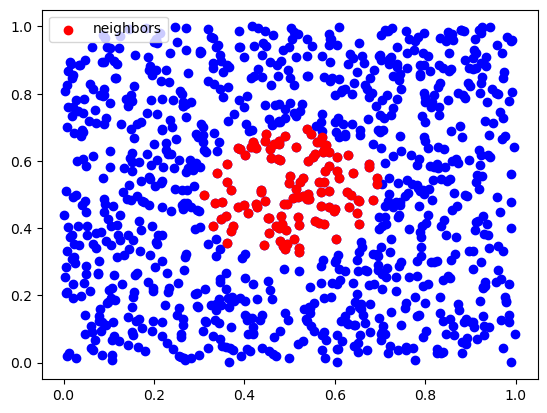
def rnn(x, X, r, **kwargs):
    """
    find r-nearest neighbors of x in X
    """
    d = distance.cdist(x.reshape(1,-1), X, **kwargs).flatten()
    return np.where(d<r)[0]

inds = rnn(x, X, 0.2)
plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r', label="neighbors")
plt.legend()
plt.show()

Exercise

What is the time complexity of both the above functions?

---

show your work

KD-trees

One of the issues with a brute force solution is that performing a nearest-neighbor query takes \(O(n)\) time, where \(n\) is the number of points in the data set. This can become a big computational bottleneck for applications where many nearest neighbor queries are necessary (e.g. building a nearest neighbor graph), or speed is important (e.g. database retrieval)

A kd-tree, or k-dimensional tree is a data structure that can speed up nearest neighbor queries considerably. They work by recursively partitioning \(d\)-dimensional data using hyperplanes.

scipy.spatial provides both KDTree (native Python) and cKDTree (C++). Note that these are for computing Euclidean nearest neighbors

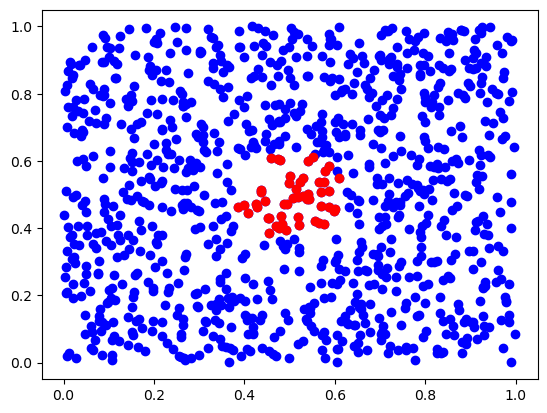
from scipy.spatial import KDTree, cKDTree

tree = KDTree(X)

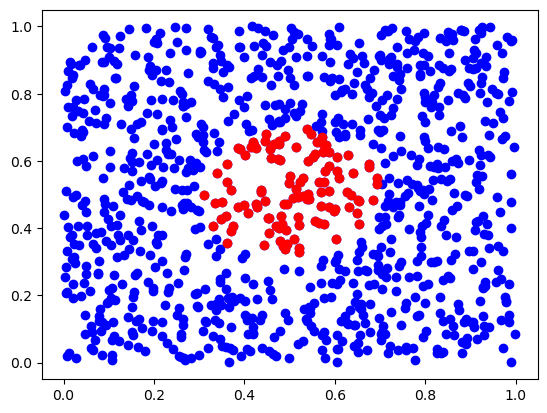
ds, inds =  tree.query(x, 50) # finds 50-th nearest neighbors

plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

inds = tree.query_ball_point(x, 0.2) # finds neighbors in ball of radius 0.1
inds = inds[0]
plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

cKDTrees have the same methods

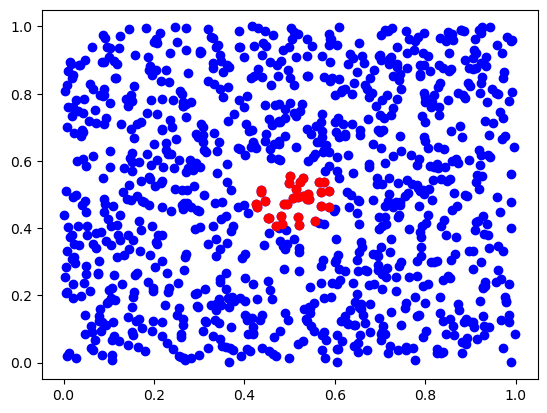
ctree = scipy.spatial.cKDTree(X)

ds, inds =  ctree.query(x, 50) # finds 50-th nearest neighbors

plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

inds = tree.query_ball_point(x, 0.1) # finds neighbors in ball of radius 0.1
inds = inds[0]
plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

Performance Comparision

import time

k=50

n = 100000
d = 2
Y = np.random.rand(n,d)

t0 = time.time()
inds = knn(x, Y, 50)
t1 = time.time()
print("brute force: {} sec".format(t1 - t0))

t0 = time.time()
tree = KDTree(Y)
ds, inds =  tree.query(x, 50) # finds 50-th nearest neighbors
t1 = time.time()
print("KDTree: {} sec".format(t1 - t0))

t0 = time.time()
ds, inds =  tree.query(x, 50) # finds 50-th nearest neighbors
t1 = time.time()
print("  extra query: {} sec".format(t1 - t0))

t0 = time.time()
tree = cKDTree(Y)
ds, inds =  tree.query(x, 50) # finds 50-th nearest neighbors
t1 = time.time()
print("cKDTree: {} sec".format(t1 - t0))

t0 = time.time()
ds, inds =  tree.query(x, 50) # finds 50-th nearest neighbors
t1 = time.time()
print("  extra query: {} sec".format(t1 - t0))

brute force: 0.0015192031860351562 sec
KDTree: 0.030165433883666992 sec
  extra query: 0.00010848045349121094 sec
cKDTree: 0.02585148811340332 sec
  extra query: 9.942054748535156e-05 sec

Ball trees

If you want to do nearest neighbor queries using a metric other than Euclidean, you can use a ball tree. Scikit learn has an implementation in sklearn.neighbors.BallTree.

KDTrees take advantage of some special structure of Euclidean space. Ball Trees just rely on the triangle inequality, and can be used with any metric.

from sklearn.neighbors import BallTree

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[15], line 1
----> 1 from sklearn.neighbors import BallTree

ModuleNotFoundError: No module named 'sklearn'

The list of built-in metrics you can use with BallTree are listed under sklearn.neighbors.DistanceMetric

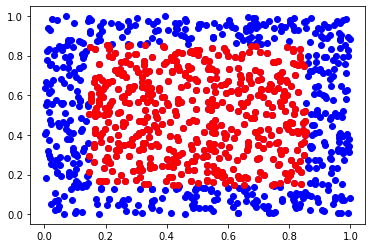
tree = BallTree(X, metric="minkowski", p=np.inf)

for a k-nearest neighbors query, you can use the query method:

ds, inds = tree.query(x, 500)

plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

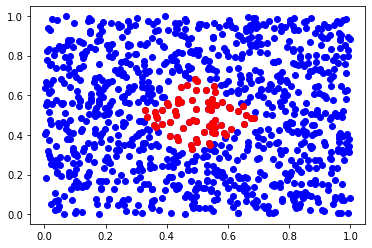
for r-nearest neighbors, you use query_radius instead of query_ball_point.

inds = tree.query_radius(x, 0.2)
inds = inds[0]

plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

tree = BallTree(X, metric='chebyshev')

inds = tree.query_radius(x, 0.15)
inds = inds[0]

plt.scatter(X[:,0], X[:,1], c='b')
plt.scatter(X[inds,0], X[inds,1], c='r')
plt.show()

Exercises

1. Compare the performance of KDTree, cKDTree, and BallTree for doing nearest neighbors queries in the Euclidean metric

2. Scikit learn also has a KDTree implementation: sklearn.neighbors.KDTree - how does this compare to the KDTree implementations in scipy?

## Your code here